計算ミス！

中学受験【偏差値30台〜40台は計算ミスが命取り】〜発達障害〜（発達障害）

プロ家庭教師のジャンプには首都圏模試偏差値40台〜50台（合不合判定模試やサピックスオープンの偏差値だと30台〜40台）の私立中学を目指す小2〜小6（発達障害やグレーゾーンが約8割です）の生徒たちがたくさんいます。（中学受験の偏差値40台の学校は進学校です。これについてはこちらのコラムのラストでお話します）

偏差値４０台といっても、入試問題は公立小で習う教科書レベルよりははるかに難しい問題ばかりです。算数だとたいていの学校は最初が計算問題になっており、小学校ではやったことがないような複雑な小数・分数が混ざった計算であったり、▢を使った問題などが出題されます。

しかもそれらの計算問題、かなりの配点が与えられています。実は偏差値４０台の中学受験こそ、大問1、特に計算問題でのミスは致命傷になることを次のデータでご理解いただきたいと思います。

↑

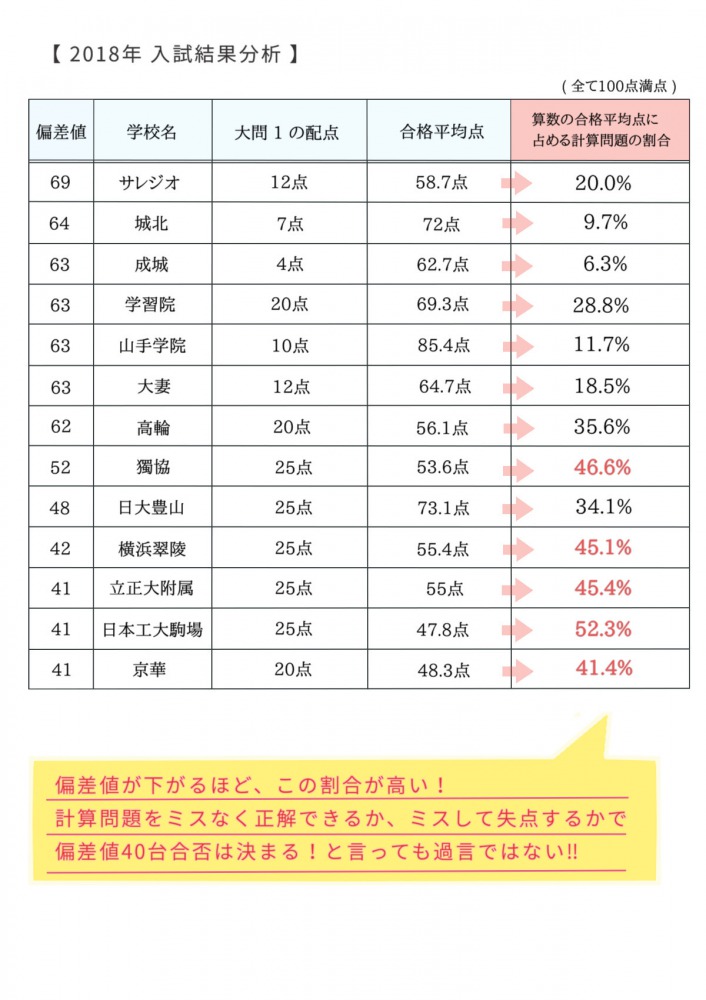
こちらのデータから偏差値４０台の入試で合格する受験生は計算問題中心の大問1を正解することで得点の約半分を稼いでいることがわかります。

ですから最初の大問1でいかにミスをせずに得点できるかがとても大切になってくるわけです。

中学受験「算数の最重要事項とは？」

しかし、ジャンプの生徒の多くは入会時、とても頻繁に計算ミスをします。彼らの多くは計算過程で見直しをしたがりません。答えが出たらそれで完了と思っている子供もたくさんいます。「きっと合っている」という思い込みで丸つけをするので間違っているのに丸をする子もいます。答えが間違っていたら正しい答えを赤で書いてその問題はもうおしまいという認識の子も多いです。お直し、解き直しといった行為は極端に嫌う傾向もあります。特に発達障害やグレーゾーンの子供たちにとっては、ASD傾向が強めでこだわりがあって解き直しを拒否したり、ADD（不注意優勢）傾向が強めで読み間違いや書き間違い写し間違いをしたり、視覚認知や聴覚認知（音韻認識）の弱さやワーキングメモリや処理速度の低さからミスをしてしまったりします。

そこで「丁寧に計算しようね」「ちゃんと見直ししようね」といったアドバイスをしても具体性がなく効果は期待できません。また高学年になるほど自分なりのやり方・ルールが身についてしまっていて、こちら側の意図する方向へ持っていくことは大変になります。ですのでなるべく低学年のうちからそういった意識付けをしていくことがとても大切になってくるわけです。

特に将来的に中学受験を視野に入れている子供にとってはどこの私立中を受けるにしても算数の大問１の計算問題は落とせないわけですから、そこに向けた計算への意識付けは低学年から行うべきなのです。目安としては２年生の９月頃から重要になってくるかと思います。なぜ２年生９月からかといいますと、そのあたりで「計算のしかたをくふうしよう」といったことを学習するからです。（ジャンプには、現在５年生や６年生のお子様でも２年生のこのあたりの計算から遡って学び直しをしている生徒さんがたくさんいます。）

具体的には２年生で以下のような計算を学びます。

①6＋12＋8や②9＋34＋6を前から順番に計算するのではなく、①なら、「まず12と8を合わせて20にして、一の位を０にする。そして6をつけたす。このほうが簡単に計算できるねー」ということに気づかせることが目的です。②も同様です。

実際の生徒さんの学校の授業ノートもご覧ください。

そこで「あぁなるほど。くふうすると楽に計算できるし速く計算もできる、しかもミスも減るんだなぁ」といった前向きな捉え方をしてくれれば以後の単元（たし算ひき算の筆算や九九の計算など２年生後半の最重要単元）も安心なのですが、「前から普通に計算しても答えは出せるし、いちいち順番を考えるのがめんどくさい」という状態になってしまうと後々大変苦労する羽目になります。

具体的には例えばこの後習う計算で、

このノートにあるような

42-7の場合だと「７を２と５に分けて42からまず2を引いて40にしてから残りの5を引く」という考え方とやり方が後の様々な計算においてとても重要になるわけですが、「筆算で解けるからいちいち7を2と5に分けなくてもいい！」となってしまうと大変です。この考えになると後々必要となる暗算力にも悪影響を及ぼします。むしろ筆算というものはなるべく使わないで済むようにトレーニングしたほうが効果的でもあるのです。（例：25×28の計算をすぐに筆算で解こうとするのではなく、4×25＝100を利用して28を4×7に分解して、25×4×7＝100×7＝700とするほうが速くて正確だったりします。）

あるいはもう少し先の『九九』でも

といった問題も、同じ意識が定着してしまっていると

①→はちにじゅうろく、はちさんにじゅうし、16と24も筆算で計算できるからそれでいいや

②→27×８も73×８も筆算で計算できるからそれでいい！

となっていく可能性があります。（偏差値４０台の中学入試では、これらの応用形として例えば　3.56×0.7−0.206×7　といった計算が出題されます。）

本来は九九の意味をきちんと理解したうえで、文章題などで絵や図を用いながら①は8×（２＋３）とまとめられること、そうすれば8×5＝４０と楽に且つ確実にミスなく答えが出せることを理解させなければいけません。②に至っては8×（27＋73）となり、8×100＝800と筆算で別々に計算するよりはるかに楽に且つ正確にミスなくできるわけですから。このように小学２年生秋以降の計算は本当に重要になってくるわけです。

いきなりですが、中学受験における算数の最重要事項を言います。

それは、さきほどから繰り返している「（楽に且つ正確に）ミスなく解く」ということです。これに「適度な速さ（書くスピード）」が加わります。

つまり「適度な速さで間違えずに計算する力」を低学年からつけていくこと。それこそが偏差値４０台の中学受験において最も大切なこととなります。

そして、「適度な速さで間違えずに計算する力」をつけるために重要なことはいくつもありますが、今回は３つに絞っていいます。

1. あーでもないこーでもない、と思考、試行をする習慣（粘り強さ）をつける
2. 絵や表や図に書きだすことができるようにする（これは１年生の算数「たしざんとひきざん」のところで「図にすると考えが残っていいね」「人やモノは〇や△といった記号を使うといいよ」など、積極的に活用することを学びます。頭の中だけで考えるのではなく、とにかく手を使って書いてみようとする子と書くのを嫌がる子との学力差は１年生から出始めます。）
3. 途中計算を丁寧に書けるようにする（３つの中で最も大切です！途中計算をきちんと書くメリットについては別コラム「途中計算」もご覧ください）

以上の３つが柱となります。この３つの柱を教える側が常に意識することが大切です。

それと同時に小学生がどんな計算ミスをしやすいのかも教える側が把握しておく必要があります。

小学生がミスしやすい計算問題

というわけで、小学生がミスしやすい計算問題BEST４を挙げてみます。

BEST４

「かけ算・わり算関連でのミス！」

BEST３

「計算の順序や手順でのミス！」

BEST２

「小数関連でのミス！」

BEST１

「分数でのミス！」

計算ミスを防ぐ具体的な方法は？

続きまして、小学生が計算ミスしないようなやり方、具体的な対策方法についてお話していきます。「視覚的配慮」「聴覚的配慮」「その他」に分けてみました。

視覚的配慮

• 途中式を下（タテ）につなげていく
• 枠や線のある教材を使う
• 色ペンでマークをする
• 符号を先に書くクセをつける
• 分数部分は÷２と書いたり②とメモする
• ノートを半分に分けて筆算スペースを作る

聴覚的配慮

• 小数点の位置は「ぴょんぴょんルール」
• 「０はオバケ」
• 合わせてガッチャン

など、キャッチ―な言い方、表現を用いる

その他

• 間違い専用ノートを作成し、どのように間違えたかを書く
• 声に出して説明させながら計算させていく
• テスト形式でやらせる
• クリア問題数を設定し、到達しなければ個別にマルバツをつけずに、間違い問題を発見させる

視覚的配慮、聴覚的配慮、その他の３つに分けてみましたが、他にも様々なアプローチはあるかと思います。

ワーキングメモリを鍛え、処理速度をアップ

そして、これら計算ミスを減らすために最も重要なことは、、、「脳のワーキングメモリを鍛える」「脳と目と手の連動、つまり処理速度をアップさせる」この２点です。

ワーキングメモリって何？

処理速度って何？

と思われる方もいるかと思います。

これらはいわゆるWISCなどの知能検査で用いられている言葉になります。

ワーキングメモリとは一時的に情報を保持してそれを使いこなす作業能力です。例えば「73946を覚えてください。そしてそれを反対から言ってみてください。」という指示に対して頭の中で73946を思い浮かべ、6から逆に4.9.3.7と一時的（数秒間）に保持した数字情報をたどっていくと思います。それをどのくらい速く正確にできるかは個人差が大きく、こういった作業が不得手だと勉強全般に影響が出てきます。聴覚的な短期記憶ともいえます。

処理速度とは、与えられた視覚情報を限られた時間内に正確に注意を払いながら書いていく処理の速さと正確さをいいます。視覚的な短期記憶ともいえます。

では、どのようにしてワーキングメモリや処理速度を鍛えればいいのか。

これも様々な方法がありますが、今回は２つご紹介させていただきます。

①タイムアタックで処理速度を上げる

十マス計算や百マス計算で時間をはかり、タイムを縮めていくトレーニングです。

②暗算や少し難しめの計算問題で頭の中の作業台を広げてワーキングメモリを鍛える

例えば３８×６。計算するとき、筆算を使わずに暗算をします。そうすると頭の中で８×６＝４８をして、４を一旦頭のどこかに留めて（覚えて）おき、次に６×３＝１８を計算すると思います。そして１８＋４＝２２と計算して、答え２２８と出すわけですが、この、４をとどめておいて同時にロクサンジュウハチを唱えて４と１８を足す作業中、頭の中でワーキングメモリを駆使しているわけです。こういった暗算を毎日一定数行うことでワーキングメモリは鍛えられていきます。

また、987165432＋234561789のようなくり上がりを連続して処理していく計算を時間内に完成させていくといった、普段はあまり行わない少し難度の高い問題をこなしていくことも処理速度やワーキングメモリを鍛えるのに効果的です。

※ワーキングメモリについてはコラム:「頭のメモ」も是非お読みください

※中学受験に関してはコラム:「母の悩み」も是非お読みください

 

(※）偏差値40台について

偏差値40台と聞いて「偏差値は50が真ん中でしょ？平均より低いからそんなに難しくないってことでしょ？」と思われる方もいらっしゃいます。しかし中学はそもそも受験にチャレンジしなくても公立中へ義務教育で自動的に進学することができるわけです。そんななかで敢えて受験のために遊びたい盛りの10歳台前半を勉強に費やす覚悟や努力をしている子供達は全国の小学生のなかでも意欲があって頑張れる子供達の集団なわけです。特に首都圏においては中学受験を目指している子供達の大半は公立小学校での学力上位組になります。すなわち、首都圏の中学受験偏差値40台というのは、全国の小学生集団でみたとき、上位グループに位置するということです。大学進学実績という観点からみたときにも、実際に都内の偏差値41〜45の私立中高一貫校の大学進学実績と、都立高校偏差値55〜58あたりの大学進学実績を比較しても殆ど差がなく、むしろ私立中高一貫校のほうがマーチ（通称MARCH。明治・青学・立教・中央・法政を指します）の合格実績はよかったりします。

また、都立高校の併願先という観点からみたときにも、例えば都立雪谷高校（偏差値59）や田園調布高校（偏差値56）の併願校として目黒学院（首都圏模試偏差値39）を受けたりするわけです。

学力上位の子供達が大半を占める小学6年上位集団の中学受験の偏差値と、学力上位の私立中高一貫校生が抜けたそれ以外の中学3年生集団の高校偏差値とは全く数値（偏差値）の比較をしても意味がないわけで、むしろ首都圏模試偏差値40台が実はとても学力上位層に位置しているんだということがわかってもらえたなら幸いです。

「発達障害×中学受験」関連コラム

• 50%以上が中学受験を検討
• 中学受験「偏差値50」2科目か4科目か
• 中学受験「偏差値40台」応用問題
• 中学受験「レベル別攻略」